Um ein Speicherobjekt nach außen hin zu beschreiben, muß man angeben, welchem Wertebereich das Objekt genügt. Bei den Standard-Variablentypen, wie Sie sie aus GFA-Basic kennen, ist das sehr einfach. Die Wertebereiche der Typen BOOLEAN, BYTE, WORD, INT, FLOAT und STRING sind schnell erläutert. Auch "Array" ist ein Typ, der vom Basic zur Verfügung gestellt wird, den man recht einfach verstehen kann, da es keine komplexe, sondern eine recht triviale Form eines Wertebereichs ist.
Der Speicher zur Aufnahme von Daten über Videokassetten aus dem letzten Kursteil war ebenso recht einfach zu erfassen. Es handelte sich um ein Array aus "Kassetten", von denen jede einzelne einige Attribute hatte: Kassettentitel, Spielzeit und eine Filmliste. Unsere Fußballwelt scheint aber bereits etwas komplexer zu werden, gibt es doch immerhin Ligen, Vereine, Fußballspieler, vielleicht auch eine Transferliste usw. Über all diese Objekte müssen Informationen im Spielstandspeicher festgehalten werden.
Um auch bei komplexen Strukturen den Überblick zu behalten, hat man einen Plantyp entwickelt, mit dem sich Strukturen grafisch veranschaulichen lassen: ER-Diagramme. "ER-Diagramm" steht für Entity-Relation-Diagramm, was auf Deutsch so viel heißt wie "Menge-Beziehung-Diagramm". Die Diagramme sind die Fortführung dessen, was man aus der Grundschule bereits kennt, wo man Mengen mit Ovalen symbolisierte.
Zum Entwerfen von Speicherobjekten für komplexere Strukturen eignen sich diese Pläne hervorragend, da man später sogar recht einfach den Sourcecode regelrecht von den Plänen abtippen kann. Man ermittelt zuvor über ein Brainstorming die Typen der Objekte, über die Informationen im Speicher abgelegt werden sollen. Für unseren Fußballmanager kommen wir schnell auf vielleicht folgende Klassifikation:
| Fußballspieler: | Das sind die kleinen virtuellen Männchen, über die wir
uns ihre Spielstärke, ihren Transferwert, ihr Gehalt usw. merken
müssen.
|
| Vereine: | Die Vereine verfügen jeweils über ein Repertoire an
Spielern, haben ein Vereinskonto, ein Stadion mit bestimmter
Größe usw.
|
| Ligen: | Die Ligen werden aus Vereinen gebildet, die in bestimmter
Reihenfolge gegeneinander antreten. Dabei gilt es stets, den
Tabellenstand zu merken. Am Ende einer Saison wechseln einige
Mannschaften durch Auf- und Abstieg die Liga.
|
| Manager: | Auch zu den Spielern, die vor dem Monitor sitzen, müssen wir
uns natürlich Informationen merken: Wie heißen sie? Welchen
Verein managen sie? Wieviele Punkte haben sie bereits erreicht?
|
| Transferliste: | Damit auch ein wenig Dynamik ins Spiel kommt, ist eine
Transferliste sehr interessant. Vereine können Spieler mit einem
Mindestgebot in die Liste eintragen, andere Vereine können
Angebote machen, woraufhin der meistbietende Verein den Spieler
bekommt. Es bietet sich also an, zwischen Angeboten (also
Einträgen in der Liste) und Nachfragen (also Angebote für
Spieler auf der Liste) zu unterscheiden.
|
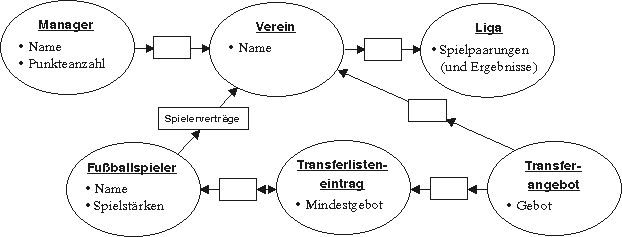
Nachdem man sich die Gedanken auf diese Weise ein wenig geordnet hat, zeichnet man sich Mengenkreise für die einzelnen Klassen. In unserem Beispiel wäre das jeweils ein Kreis für die Fußballspieler, die Vereine, die Ligen, die Manager, die Transferlisteneinträge und die Transferangebote. Anschließend gilt es dann festzuhalten, wie die Objekte aus den einzelnen Klassen zueinander in Beziehung stehen. Bevor erklärt wird, wie man diese Dinge festhält, sollen Sie nun bereits einen Blick auf das fertige ER-Diagramm für unserere Fußballwelt werfen:

Die einzelnen Mengenkreise sind beschriftet mit dem Typbegriff der Objekte, die zu der jeweiligen Menge gehören. Die Menge der Vereine ist beispielsweise mit dem Begriff "Verein" beschriftet.
Man kann nun unterstützend bereits beliebige Attribute der Objekte innerhalb der Mengenkreise aufzählen, so wie das im Strukturbild bereits mehrfach gemacht wurde. Zu jedem Manager müssen Name und Punktezahl gespeichert werden, Fußballspieler haben Namen und Spielstärken, für jede Liga gilt es sogar, sich Informationen einer etwas komplexeren Struktur zu merken: Wie lauten die Spielpaarungen? Welcher Spieltag ist der aktuelle? Wie waren die Ergebnisse der bereits ausgetragenen Spiele? Diese Dinge sind in diesem groben Überblick noch nicht genauer aufgeschlüsselt.
Dort jedoch, wo es um Fragen geht, die sich nicht auf Objekte eines einzelnen Typs beziehen, sondern wo mehrere Typen in Beziehung gebracht werden, geht man zur Darstellung andere Wege. So gehört ja jeder Fußballspieler beispielsweise zu einem Verein. Nun könnte man in die Attributliste der Fußballspieler das Attribut "Verein" eintragen, und sich darin merken, zu welchem Verein der Spieler gehört. Man könnte genauso gut aber in die Attributliste der Vereine das Attribut "Spielerauflistung" eintragen, und dort jeweils die Spieler aufzählen, die zum jeweiligen Verein gehören. Beides ist möglich. Man zeigt aber stattdessen lieber direkt im Bild, daß Fußballspieler und Vereine in Beziehung stehen und zeichnet diese Beziehung ein: als Rechteck, welches durch jeweils eine Linie mit der Menge der Fußballspieler und der Menge der Vereine verbunden ist. Im Bild ist dieses Rechteck mit "Spielerverträge" beschriftet.
Man hat als Form das Rechteck gewählt, weil sich eine solche Relation (Relation = Beziehung) jeweils als Tabelle angeben läßt, und Tabellen ebenfalls rechteckig sind:
| Verein \ Spieler | Matthäus | Klinsmann | Kahn |
| Dortmund | |||
| Stuttgart | X | ||
| München | X | X |
Diese Tabelle ist eine solche Tabelle, in der Spielerverträge aufgelistet werden. Zu jedem Spieler ist angekreuzt, bei welchem Verein er unter Vertrag steht.
Bevor auf die anderen Relationen im Bild eingegangen wird, sei zunächst noch die Pfeilung erläutert. Mit den Pfeilen wird ausgedrückt, ob jeder Spieler einem Verein angehören muß, oder nicht, oder ob er sogar genau einem Verein angehören muß. Dazu gibt es folgende Pfeilungsmöglichkeiten:

Pfeile in die umgekehrte Richtung sind natürlich ebenfalls möglich. Ihre Bedeutung ist dann entsprechend in die andere Richtung analog.
Dementsprechend sagen die neben den Spielerverträgen eingezeichneten Beziehungen im Strukturbild folgendes aus:
Das Entwerfen von zum Problem passenden ER-Diagrammen erfordert ein wenig an Übung. Es gibt auch noch einige weitere Symbole, die man in ER-Diagrammen einsetzt, um bestimmte Zusammenhänge anschaulicher darzustellen. Darauf soll aber an dieser Stelle nicht näher eingegangen werden.
Nun bauen wir auf den bisherigen Überlegungen basierend einen Speicher zur Aufnahme der Informationen unserer Fußballwelt.
Der Entwurf des Spielstandspeichers