

von Olaf Piesche und Christian Eyrich

Überblick:
Wie lange läuft ein Bild?
Binäre Kodierungen
Lempel-Ziv-Welch
Weitere Methoden, Daten zu komprimieren
Downsampling
Hallo, alle zusammen. Willkommen im zweiten Teil unseres Artikels über Grafikformate.
Und ohne lange Vorreden stelle ich jetzt einfach mal eine Behauptung in den Raum: Die meisten Bilder sind in Wirklichkeit viel größer, als es den Anschein hat und man auf den ersten Blick sieht.
Neinneinnein, Ihr braucht jetzt nicht Eure Grafikviewer rauszukramen und in euren Bildern nach den versteckten Daten zu suchen. Was ich meinte, ist die einfache und allgemeinhin bekannte Tatsache, daß die meisten Bildformate heute eine Komprimierung benutzen. Ein Beispiel soll den Sinn des ganzen verdeutlichen:
Nehmen wir ein True-Color-Bild mit 24 Bit Farbtiefe, also 16,78 Millionen Farben und einer Größe von 1024*768 Pixeln an. Dieses Bild - 24 Bit = 3 Bytes pro Pixel - wäre also schlappe 2,3 Megabytes groß - hundert Stück davon und die kleine 240er Platte ist voll; zur Übertragung eines solchen Bildes mit einem 14400er Modem würde man ca. eine Viertelstunde brauchen.
Deshalb wurden im Laufe der Zeit - einer Zeit, als zwei-Gigabyte-Platten noch nicht wie alte Bücher auf dem Flohmarkt verhökert wurden - Algorithmen entwickelt, um die Datenmengen zu reduzieren. Und genau diesen Algorithmen wollen wir uns in diesem zweiten Teil unseres Artikels widmen. Wie kommt es, daß z.B. ein 256farbiges GIF-Bild mit 640*480 Pixeln, das unkomprimiert über 300 Kilobytes groß wäre, auf der heimischen Platte mit häufig einem Drittel dieses Platzes auskommt?
Der einfachste Komprimierungsalgorithmus ist wohl die RLE - Run Length Encoding, oder zu gut deutsch Lauflängenkodierung. Diese basiert auf der einfachen Tatsache, daß sich in vielen Bildern Pixel mit demselben Wert wiederholen. Und genau das kann man sich sparen.
Ein einfaches Beispiel: Ein Bild enthält folgende Pixelfolge, byteweise dargestellt:
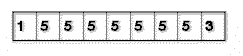
Irgendwo befinden sich also 7 Pixel, die alle den Wert 5 haben. Mit einer einfachen RLE kodiert, sieht das dann z.B. so aus:
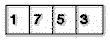
Heraus kommen 2 Bytes, also 5 gespart. Ganz so einfach ist es natürlich nicht, denn woran soll das Programm, das das Bild hinterher laden will und somit wieder dekodieren muß, wissen, daß die 7 ein Wiederholungszähler und kein Pixelwert ist? Deshalb werden vor solche Wiederholungen Kennungen gesetzt, die sonst in den komprimierten Bilddaten nirgendwo vorkommen. Am weitesten verbreitet ist hier die Methode, die Anzahl an Wiederholungen für einen solchen Block durch das setzen von Bit 8 zu kennzeichnen. D.h., ist in einem Byte Bit 8 gesetzt, geben die unteren 7 Bit dieses Bytes die Anzahl an sich wiederholenden Pixeln an (woraus sich für einen komprimierten Block eine maximale Länge von 128 Pixeln ergibt), ansonsten die Anzahl an unkomprimierten Bytes, die folgen.
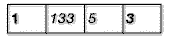
Trifft das ladende Programm also im komprimierten Bild in diesem Beispiel auf die 133, dann weiß es, daß 5 (=133-128) mal das nächste Byte wiederholt werden soll. Nun wurden also 7 Bytes auf 2 Bytes reduziert.
Beispiele für mit einer RLE gepackte Bildformate sind BMP, PCX und STAD. Besonders bei PCX erkennt man auf den ersten Blick eine schlechte RLE, da die gepackten Bilder häufig größer sind, als es die ungepackten Bilddaten eigentlich wären (und das will was heißen, nämlich, daß die Programmierer vieler Programme, die solche Bilder erzeugen, sogar zu faul sind, eine Überprüfung auf eine solche Vergrößerung der Bilddaten auszuführen ;-)) - auf eine solche "Expansionskomprimierung" kann man getrost verzichten. Bilder des ST-Malprogrammes STAD sind da schon besser gepackt, da die Bilder immer monochrom vorliegen (also meist schwarze und weiße Flächen enthalten) und außerdem sowohl zeilenweise als auch spaltenweise (also senkrecht) gepackt sein können.
RLE ist zwar die einfachste Komprimierungsmethode, aber leider Gottes auch die uneffizienteste - sich wiederholende Pixelfolgen kommen in den meisten Bildern nicht in dem Maße vor, daß hier berauschende Einsparungen zu machen wären.
Also forschte der findige Programmierer weiter und erfand noch ausgefuchstere Komprimierungsverfahren.
Diese Methode wird von verschiedenen Komprimierungsalgorithmen genutzt und basiert auf der Tatsache, daß z.B. in Bildern mit 8 Bit Farbtiefe nicht immer 8 Bit benötigt werden, um einen Pixelwert zu speichern (z.B. benötigt man für den Wert 125 ja nur 7 Bit).
Sie hat nicht die Nachteile der RLE und komprimiert so ziemlich alles, was ihr unterkommt, um Faktoren, die meist jenseits von 30% liegen. Binäre Kodierungen sind allerdings ein ganzes Stück komplizierter als z.B. die RLE und die Ausführung ist darum natürlich etwas rechenaufwendiger. Ein solcher Algorithmus könnte, in einfacher Form beschrieben, ungefähr folgendermaßen vorgehen:
Die Daten werden in Blöcken (z.B. zu je 8 Byte) abgelaufen und die Werte darin in eine sog. Codetabelle einsortiert. Bei einem Block
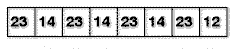
erhält man also z.B. so eine Codetabelle:

Danach werden die Werte im Block durch ihre Referenzwerte, also die aus der Codetabelle ersetzt:
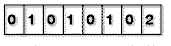
Wie man sieht, ließe sich der so vorliegende Block nun hervorragend bitweise codieren, da man z.B., um die Werte darzustellen, die nun im Block stehen (zwischen 0 und 2), nur noch 2 Bit benötigt, und nicht mehr 8 Bit, wie vorher, als die Werte noch zwischen 0 und 255 rangieren konnten. Für jeden Block wird dann also festgelegt, wieviele Bits für einen Pixelwert zuständig sind (in unserem Beispiel 2) und die Werte dann bitweise abgelegt:
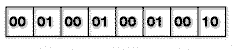
Das ganze schiebt man dann eben noch so zusammen, daß wirklich nur noch 2 Bits pro Wert verwendet werden. Mit Darstellung der Bytegrenzen sieht das also so aus:
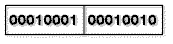
In diesem Block wurden also Werte, die sich nur mit 8 Bit darstellen ließen, auf 2 Bit reduziert. Für 8 Werte (Bytes) wurden ursprünglich 64 Bit benötigt, nun nur noch 16 Bit, also 2 Bytes. Dazu kommt dann noch die Codetabelle, die ebenfalls Bitweise abgelegt wird (für die Darstellung des Wertes 23 benötigt man nur 5 Bit) und in unserem Fall also 2 Bytes groß wäre. Also eine Reduktion von 8 auf 4 Bytes, mit anderen Worten um ca. 50%.
Die Komprimierungsrate kann sich aber mit anderen Blockgrößen und -inhalten stark verändern; wenn z.B. in einem 64 Bytes langen Block nur 10 verschiedene Pixelwerte vorkommen würden, könnte die Kodierung die Daten auf 64*4 Bit, also 256 Bit, was 16 Bytes entspricht, reduzieren. Das entspricht einer Komprimierung um ca. 75%, zuzüglich der Codetabelle. Außerdem läßt sich vielleicht die Codetabelle noch reduzieren und wieder bitweise abspeichern, so daß man höhere Komprimierungsraten erhalten kann. Nun sollte man vielleicht die Codetabellen ihrerseits wieder in eine Liste eintragen und durch zu den komprimierten Datenblöcken gehörige Referenzwerte ersetzen, um keine identischen Codetabellen mehrfach in der Datei halten zu müssen.
Man sieht hier, daß die Effizienz einer binären Kodierung in dieser Form nicht so stark von den zu packenden Daten abhängt wie die einer RLE. Trotzdem kann man die Komprimierungsraten noch steigern: so verwendet z.B. das JPEG-Bildformat eine Kombination mit einer RLE und baut die binäre Kodierung in Form eines binären Baumes auf (Huffman-Kodierung). Denkbar wäre auch eine Modifizierung, in der unterschiedliche Blockgrößen verwendet werden.
Ein Vorteil ist, daß die Kodierung selbst in dieser einfachen Form auch mit sich wiederholenden Bytefolgen recht gut zurechtkommt. Eine Wiederholung von 32mal dem Wert 56 z.B. würde hiermit von 32 Bytes auf 32 Bit, also 2 Bytes, plus 1 Byte für die "Codetabelle" (die hier ja nur einen Wert enthalten würde) gepackt. Also eine Komprimierung dieses Blockes um fast 90%.
Einer der im Computergrafikumfeld am häufigsten verwendeten Algorithmen ist der LZW-Algorithmus. Die allgemein bekanntesten Stellen dürften GIF, TIFF, V.42bis und PostScript Level 2 sein.
Im Gegensatz zur Huffman-Kodierung ist der LZW selbst brandneu und sein Ursprung auch noch recht frisch. 1977 setzten sich Abrahamn Lempel und Jakob Ziv zusammen und erfanden den Urvater der LZ-Familie. Abgeleitet vom Jahr nennt man diesen Zweig LZ77, dessen Implementationen sich in den bekannten Textkompressions und Archivierungsprogrammen wie LHarc, ZIP, Zoo oder ARJ finden. Die LZ78 Algorithmen finden sich häufiger in Implementationen, welche auf Binärdaten abzielen - z.B. Bilder.
Und nun kommts (sagt der Fielmannkerl): 1984 modifizierte Terry Welch den LZ78-Algorithmus für den Einsatz in High-Performance-Disk-Controllern. Das Ergebnis war der LZW, der wohl bekannteste aller Lempel-Ziv-Kompressoren.
LZW gehört zu der Gruppe der Dictionary-basierten Kodierungen. Der LZW ist im Grunde ein sehr simpler Algorithmus.
Der Algorithmus erstellt ein "Data Dictionary" (was sich wohl am besten und wörtlichsten mit "Datenwörterbuch" übersetzen läßt) aus den Daten, die im unkomprimierten Datenstrom vorkommen. Muster (zusammenhängende Bytes) in diesem Strom werden in ein Dictionary verfrachtet und durch Verweise auf den jeweiligen Eintrag ersetzt (deshalb nennt man die Gruppe dieser Algorithmen auch "substitutional"). Dieses Wörterbuch wird ALSO on-the-fly aufgebaut Und zwar sowohl vom Encoder als auch vom Decoder - damit braucht es überhaupt nicht mit abgespeichert zu werden!
LZW beginnt mit einem Dictionary von 4 KB. Die ersten 256 Einträge werden mit den Bytes 0 bis 255 vorbelegt. Neue Strings werden durch Anhängen der aktuellen Eingabe K an den String w generiert.
Folgender Pseudocode soll die Vorgehensweise beschreiben - ich denke, das ist unkomplizierter und selbst für Nicht-Programmierer eingängiger als langes rumreden:
K initialisieren
Schleife
Lese Byte und hänge es an String K
wenn K in der Tabelle
Position des Strings in Tabelle merken
ansonsten
K an als neuen Eintrag in Tabelle
gemerkte Position ausgeben
K gleich letztem Byte setzen
Ende Schleife
Ein Beispiel:
Eingabe: /WED/WE/WEE/WEB
usw.
| Bytes Eingabe: | Code Ausgabe: | Neue Codes und zugehörige Werte: |
| /W | / | 256 = /W |
| E | W | 257 = WE |
| D | E | 258 = ED |
| / | D | 259 = D/ |
| WE | 256 | 260 = /WE |
| / | E | 261 = E/ |
| WEE | 260 | 262 = /WEE |
| /W | 261 | 263 = E/W |
| EB | 257 | 264 = WEB |
| <END> | B |
Natürlich ist die hier erreichte Komprimierung eher lächerlich und jeder Mensch würde erstmal /WE ablegen und bei jedem Vorkommen einsetzen. Dann würden 7 Byte und nicht 14 Byte Output erzeugt. Aber erst mal ist dieses Beispiel recht kurz und zweitens mache man so ein Vorgehen erst mal dem Computer klar. Naja und außderdem steigt die Kompressionsrate bei längeren Beispielen noch ganz gut. Im allgemeinen darf mit Raten um die 50% gerechnet werden.
Wenn dann alle 4096 Einträge des Dictionaries voll sind, wird dann ein sog. Clearcode ausgegeben, die Tabelle wieder bis Eintrag 255 initialisiert und von vorne begonnen.
Wie gesagt, der Algorithmus ist einfach, die Implementation jedoch ist recht schwer, zumindest wenn sie effizient sein soll. Abwandlungen gibt es viele, z.B. werden manchmal nicht nur ein Byte, sondern gleich zwei an den String angehängt und verglichen, im Dictionary gesucht kann auch mit unterschiedlichen Methoden. GIF z.B. nimmt nicht fest ein Byte als Symbol, sondern die Anzahl Bytes, die ein Pixel darstellen, also auch mal ein Bit oder deren vier. Natürlich kann auch die Maximalgröße des Dictionary erhöht werden, oder es wird nicht aufgebaut, indem jeweils ein Byte angehängt, sondern zwei Muster zusammengehängt (LZMW-Variante). Oder andere Varianten beobachten die erreichte Kompression und verwerfen bei sinkender Kompressionsrate die am wenigsten genutzten Wörterbucheinträge.
Preisfrage: Was ist die einfachste Methode, ein Bild in der Größe zu reduzieren? Ganz einfach: Grafikdaten weglassen.
So dümmlich sich diese Antwort auch anhört, gibt es doch verschiedene Bildformate, die gerade diese Methode verwenden, z.B. JPEG und Kodaks Photo-CD Format. Der Fachausdruck ist natürlich nicht einfach "weglassen", sondern
Dieser Schritt beruht auf der Ausnutzung des "Fehlers" des menschlichen Gehirns, Farbintensitätsunterschieden gegenüber nicht so empfindlich wie für Helligkeitsunterschiede zu sein. Da das Bild zunächst in ein Farbsystem umgerechnet wird, welches diese Informationen getrennt abspeichert, wie YCbCr oder YIQ, kann dieses Downsampling recht einfach stattfinden. Der Y-Teil bleibt vorhanden und der weggefallene CbCr-Teil wird bei der Darstellung interpoliert.
In folgender Tabelle ist ein 2:1:1 Sampling aufgezeigt, alleine hierdurch wird schon eine Kompression auf 50% erreicht.
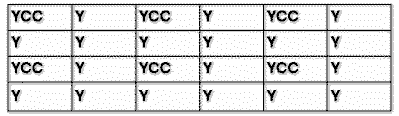
Zusätzlich können noch weitere Routinen wie RLE, Huffman oder LZW angewandt werden, um die abzuspeichernde Menge weiter zu drücken.
Wie sich jeder bei PCD-Bildern überzeugen kann, ist der Unterschied erst bei nahem Betrachten sichtbar. JFIF-Dateien sollten hierfür nicht zu Rate gezogen werden, da hier noch ein weiterer verlustbehafteter Schritt angewandt wird.
Oft taucht noch der Begriff Pixel Packing auf und es wird ein netter Kompressionsalgorithmus dahinter vermutet. Nunja, wenn man will, kann man es so bezeichnen. Es sind wahrscheinlich die gleichen Leute, die Doodle als Grafikformat bezeichnen. Was Pixel Packing nun ist, habe ich aber schon in Teil 1 beschrieben (siehe Pixelpacking).
So, im nächsten Teil unserer Serie wollen wir deren Namen endlich einmal gerecht werden und wichtige und interessante Grafikformate auseinanderpflücken und deren Besonderheiten aufzeigen.

