


Von Hauke Wessels

Dies ist der letzte Teil über dynamische Datenstrukturen. Nachdem wir in den beiden vorangegangenen Teilen erfuhren, was dynamische Datenstrukturen sind und was eine verkettete Liste ist, lernen wir in diesem Teil einiges über das Verwalten von Bäumen.
Übersicht:
Ein Fehlkauf ...
Das fleißige Eichhörnchen
Mama, 's Eichhörnchen ist tot...
AVL-Bäume - Sortieren mit Merker
Ausgleichen - aber wie?
Jetzt endlich: Einfügen
Löschen im AVL-Baum
Epilog
Literaturhinweise
Nachdem wir uns vor 2 Monaten von einer netten Verkäuferin eine CD von Loreena McKennitt aufschwatzen lassen haben, haben wir inzwischen den Fehler gemacht, sie uns einmal anzuhören .
Da sie (wohlgemerkt die CD, nicht die Verkäuferin; nicht, daß wir uns da mißverstehen...) bereits in unseren schönen binären Baum eingetragen wurde, muß sie dort wieder entfernt werden. Schließlich hat sie inzwischen der ahnungslose Junge von nebenan ...
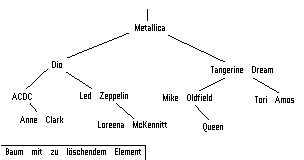
Da wir nach der letzten CD noch keine weiteren eingefügt haben, besitzt der Knoten mit "Loreena McKennitt" noch keine weiteren Kinder (Nachfolger) und ist daher sehr leicht zu löschen, indem wir einfach den "rechts"-Zeiger vom Vaterknoten als leer markieren und den Speicherblock wieder freigeben.
In einem weiteren einfachen Fall besitzt der zu löschende Knoten nur auf einer Seite einen Teilbaum, der andere Teilbaum ist leer. Dann können wir das betreffende Element einfach gegen den Kind-Knoten ersetzen und den ersetzten Knoten freigeben. Dies ist in unserem Beispiel z.B. beim Löschen von "ACDC" der Fall.
Ganz so einfach geht das aber leider nicht immer. Möchten wir z.B. den Knoten "Metallica" im Baum löschen, müssen wir irgendeinen Ersatz finden, der den Platz des gelöschten Knotens einnimmt.
Am einfachsten, weil sich nichts wirklich ändern würde, wäre es, wenn wir an die Stelle das nächst größere oder das nächst kleinere Element setzen würden. Alle Elemente, die kleiner waren, bleiben auch weiterhin kleiner, alle größeren Elemente bleiben größer.
Weil der binäre Suchbaum ja sortiert ist, können wir den direkten Vorgänger bzw. Nachfolger auch sehr leicht finden. Wir versuchen es mit dem Vorgänger:
Da in jedem linken Teilbaum alle Elemente "kleiner" sind als das Element im Knoten darüber und das "größere" Elemente stets in dem rechten Teilbaum eingefügt wird, finden wir den direkten Nachfolger in der Sortierung, indem wir den am weitesten rechts stehenden Enkel in linken Sohn suchen.
In diesem Fall wäre das "Loreena McKennitt".
Da der direkte Vorgänger keinen rechten Sohn-Knoten haben kann (sonst gäbe es ja noch ein Element dazwischen), ersetzen wir ihn einfach durch seinen linken Sohn. In unserem Beispiel also durch eine Markierung (NULL).
Anschließend setzen wir den Eintrag einfach an die Stelle des zu löschenden Elements.
Es sind also folgende Schritte notwendig:
Da dieser ATOS-Ausgabe die kommentierten C-Quelltexte beiliegen, verzichte ich hier darauf, sie nochmal anzuzeigen.
Stellen wir uns einmal vor, wir wären ein junges, aufstrebendes Eichhörnchen, das gerade eine Ausbildung als Nuß-Lager-Verwalter abgeschlossen hat und nun ein eigenes Lager verwaltet.
Binäre Bäume gehören in der Ausbildung von Nuß-Lager-Verwaltern zum Standard, schließlich wollen die sich auch nicht zu Tode klettern und Nüsse wiegen schon einiges, wenn man sie über Äste hieven muß.
Unsere frisch angetraute Eichhörnchen-Ehefrau ist so aufgeregt, daß sie nicht ruhig bleiben kann und schon vorab eine Namensliste aller neuen Kunden macht. Strebsam, wie sie ist, hat sie diese Liste natürlich alphabetisch geordnet ...
Und prompt kommen die neuen Kunden auch der Reihe nach, um ihre schwer zusammengesammelten Nüsse in ein neues Lager zu geben.
Wie wir sicherlich schon vermuten, passiert das Schlimmste. Der schöne binäre Baum "entartet" zu einer verketteten Liste und damit müssen wir als Eichhörnchen ganz schön weit laufen.
Aber zum Glück erinnern wir uns - kurz bevor uns schwarz vor Augen wird - an die alte Legende des Lagerverwalter-Eichhörnchens "Oskar", der sich einmal dem selben Problem gegenübersah. Er löste es, indem er kleine Leitern von Ast zu Ast legte und andere Äste als gesperrt markierte. Er zählte ab, wie viele Ebenen es von jedem Knoten aus noch gab und versuchte, jeden Teilbaum möglichst "ausgeglichen" zu halten.
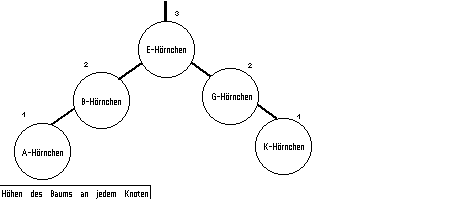
Damit verbrachte er jeden Abend etwas Zeit, um alles optimal zu halten. Sein Sohn (Willi) verbesserte dann das Verfahren, indem er Markierungen an jeder Astgabel vergab, ob, und wenn ja, wie die Unterbäume ausgeglichen sind. Er wollte damit die Zeit abends sparen und gleich während des Einsortierens das Ausgleichen erledigen.
Dazu verwendete er halbe und ganze Eicheln. Eine halbe Eichel bedeutet, daß der linke Teilbaum um eine Ebene tiefer ist als der rechte. Eine ganze Eichel bedeutet, daß der rechte Teilbaum um eine Ebene höher ist, als der linke. Ist keine Eichel da, so bedeutet daß, das der linke und der rechte Teilbaum gleich tief sind. Durch dieses Verfahren hatte Willi nicht nur immer mal wieder einen Snack zwischendurch - schließlich müssen die Eicheln ja halbiert werden - sondern konnte auch eher Schluß machen als sein Vater, denn sobald ein Teilbaum, der sowieso schon um eine Ebene tiefer ist (halbe oder ganze Eichel), wußte Willi, daß ausgeglichen werden mußte.
(Anmerkung aus dem Eichhörnchenbuch: wem Eicheln zu bitter sind, der kann hier auch Kastanien verwenden).
Bäume mit diesem Verfahren nennt man AVL-Bäume, nach den Eichhörnchenforschern, die dieses Verfahren zuerst beschrieben haben. Da wir keine Eicheln haben, wird ein Integerwert ("Balancefaktor") verwendet. Ein negativer Wert bedeutet, daß der linke Teilbaum tiefer ist, ein positiver, daß der rechte tiefer ist und 0 bedeutet, daß beide Teilbäume genau gleich tief sind. Wir können mit dem Integer sogar anzeigen, um wieviel einer der Teilbäume tiefer ist, als der andere.
Wir setzen hierbei fest, daß 2 Teilbäume maximal um eine Ebene unterschiedlich sein dürfen, steigt der Wert auf 2, so müssen wir Äste umhängen.
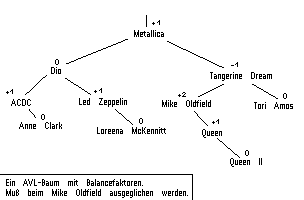
Wir haben also nun folgende Struktur "Knoten":
typedef struct knoten
{
int cd_nr; /* die CD-Nummer */
char titel[41], /* Der CD-Titel */
gruppe[41]; /* Die Gruppe */
int avl; /* "Balancefaktor" */
struct knoten *links; /* Zeiger auf den linken Teilbaum */
struct knoten *rechts; /* Zeiger auf den rechten Teilbaum */
} Knoten;
Wann müssen wir jetzt diesen Balancefaktor "avl" setzen und neu berechnen?
Der Balancefaktor muß bei jedem Einfügen neu berechnet werden, da ja immer ein Element dazu kommt und so mindestens der Knoten direkt darüber seine "Balance" ändert.
Es kann sich allerdings nur maximal der Balancefaktor aller Knoten auf dem Weg zwischen Wurzel und der Stelle, an der das Element eingefügt wird, ändern. Alle anderen Knoten sind mit dem Element ja nicht verbunden.
Den Weg zum Platz des Elements gehen wir ja sowieso (rekursiv), wenn wir den Platz zum Einfügen suchen (wie beim binären Baum), also kann man hier nach dem Rekursionsaufruf auch gleich den Balancefaktor für alle durchwanderten Knoten setzen.
Um herauszufinden, ob sich der Balancefaktor ändert, müssen wir wissen, ob der Baum unterhalb überhaupt seine Höhe verändert hat. Ist dem nicht so, so kann sich auch die Balance des aktuellen Knotens nicht geändert haben. Hat sich die Höhe geändert, so muß kontrolliert werden, ob der neue Balancefaktor im Bereich -1 und 1 ist. Erst bei einem neuen Balancefaktor von 2 (bzw. -2 für den linken Teilbaum) müssen wir ausgleichen.
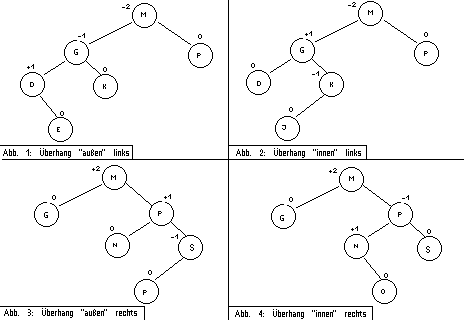
Es werden obige 4 Fälle von Unausgeglichenheit unterschieden:
Und wie wird nun ausgeglichen?
Man spricht von "Rotation", da man sich das Ausgleichen so vorstellen kann, daß die Knoten an einer Rolle hängen, und man dann an den beiden Enden gleich stark zieht, die gleich tief sein sollten. Die Rolle wird immer dort angelegt, wo der Wert gleich 2 (bzw. -2) ist.
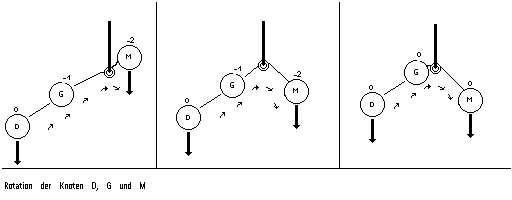
Wird dabei ein "innerer" Knoten (Knoten a) unter der Rolle durchgezogen, so wird dieser an den neuen, rechten Sohn als linker Sohn angehängt:
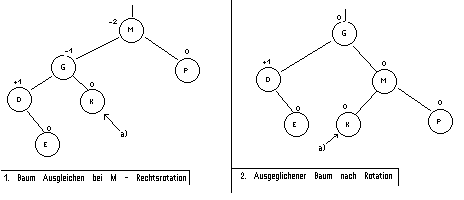
Etwas komplizierter wird es, wenn der Überhang in "mittleren" Teilbaum von links bzw. rechts ist:
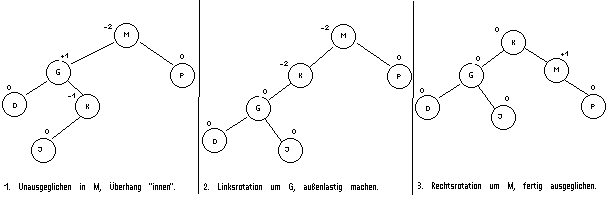
Hier muß 2-mal rotiert werden, einmal um den Überhang nach "außen" zu bekommen, und dann die Rotation wie oben zum Ausgleich.
Nachdem wir jetzt wissen, wie wir den Balancefaktor setzen und wie wir ausgleichen, können wir uns endlich an das Einfügen wagen. Es sind folgende Schritte erforderlich:
Auch dieser Quelltext ist dem Archiv beigefügt, so daß ich ihn hier ebenfalls nicht nochmal aufführe. Es wird beim Einfügen unterschieden zwischen hoeher_links() und hoeher_rechts(), da ja jeweils in unterschiedlichen Kindknoten (einmal links, einmal rechts) nach den avl-Werten unterschieden werden muß. In diesen beiden Funktionen wird abgefragt, wie ausgeglichen werden muß.
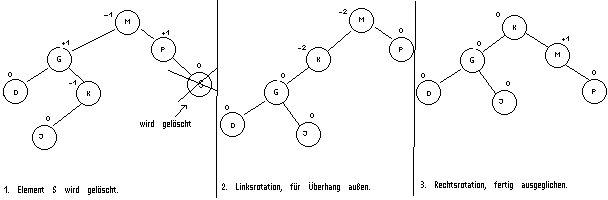
Auch das Löschen funktioniert natürlich im AVL-Baum. Allerdings muß auch hier nach dem Löschen des Elements ausgeglichen werden, und zwar auf andere Weise wie beim Einfügen: Die Tiefe des Baums wird evtl. um 1 verringert, und danach muß geprüft werden, ob der Baum neu ausgeglichen werden muß. Auch hier gilt wieder, daß das zu löschende Element wie beim bin. Baum durch den Vorgänger ersetzt wird und der Baum nur auf dem Pfad zum Vorgänger ausgeglichen werden muß.
Auch wenn die Artikelteile leider nicht direkt nacheinander erschienen sind, so hoffe ich doch, daß sie einigermaßen unterhaltsam und verständlich war, so daß wir uns in einer der nächsten Ausgaben auf generische Programmierung stürzen können.

